ABSTRACT
In this paper we explore the efficiency of various ways of expressing the form and meaning of natural language utterances as context-free grammars. We concentrate on the top-down parsing strategy employed in SpeechWorks 6.5, a strategy common to many systems. As with other search-based parsers, the key to efficiency is to limit the uncertainty of the parser at any given stage by reducing non-determinism in the grammar. Here we study the effects of different expressions of the same grammar in terms of efficiency. We also describe a methodology for transforming a source grammar into a more efficient expression of the same forms and meanings.
INTRODUCTION
Sophisticated spoken dialogue applications rely on the ability to interpret a wide range of user utterances. The usual result is a complex natural language grammar expressing both what someone can say to the system and what the system will understand them to mean. Complex grammars can lead to bottlenecks in processing if they are not expressed in an efficient way. This paper concentrates on the notion of parsing as computation in which the programs are grammars. As with other forms of programming, grammars expressing the same thing can be encoded in more or less efficient forms. As with most other problems in spoken language recognition and understanding, the fundamental principle is the reduction of non-determinism. In this paper, we will show how this can be accomplished in a principled way.
We begin with a survey of the SpeechWorks architecture for
recognition and interpretation. Next,
we provide the standard algorithm for top-down search-based parsing. We briefly discuss the role of semantic
interpretation, and then move on to a description of how grammars can be
optimized for top-down search-based parsing.
We provide empirical evidence in terms of comparative run times for
simple, equivalent grammars. We
conclude with a discussion of general techniques for optimizing grammars for
top-down search-based parsers.
RECOGNITION AND PARSING PASSES
The SpeechWorks 6.5 architecture [1] for extracting meaning from user
utterances involves three passes, including one acoustic and statistical
language model pass and two context-free grammar-based passes.
First Pass: Decoding Operates forward to construct a word
graph. Scores are determined by
successively refined acoustic models and a bigram language model.
Second Pass: Parsing Operates backwards to extract parses for the
n-best word string hypotheses that are accepted by a specified context-free
grammar.
Third Pass: Interpretation Evaluates semantics for parses generated in the
second pass. Grammars are allowed to
re-score hypotheses on the basis of semantics.[1] Word strings with equivalent semantics are
conflated before confidence scores are computed.
The final result to be processed by the dialog engine is a ranked list of
semantic hypotheses in the form of key-value pairs. Subsequent processing can re-score these hypotheses further using
context-specific information, such as user profiles, time of day, availability
of requested information, etc.
CONTEXT-FREE GRAMMARS
The context-free grammar paradigm has been thoroughly studied in the
formal languages and automata theory literature (for example, see [2] for a
range of definitions and theorems). A
context-free grammar is essentially a finite collection of phrase structure
rules. More formally, we assume a set Word of words
(often called terminals), a set NonTerminal of non-terminals,
and a finite set Rule of grammar rules, where each
grammar rule is of the form (C => X1 … Xn) where C is a non-terminal and
each of the Xi is either a non-terminal or a word.
Each grammar defines a set of
parse trees. The set of trees, Tree, is defined to
be the least set such that Word Í Tree
and such that [C T1 … Tn] Î
Tree if C Î
NonTerminal, n ³ 0, and T1,…,Tn
Î Tree. For a tree [C T1 … Tn], the
non-terminal C is said to be the root.
The yield of a tree is defined by yield(w) = w
if w is a word, and yield([C T1 … Tn] = yield(T1) …
yield(Tn); this is essentially the sequence of words appearing in
the tree read left to right. A parse
tree is a tree every node of which was derived by a rule. More formally, a tree [C T1 … Tn] is
a parse tree if (C => root(T1)
… root(Tn)) is a grammar rule and T1,…,Tn are themselves
parse trees or single words. If we take
the yields of all of the parse trees for a grammar rooted at a given
non-terminal C (often called the start symbol or root category),
we have what is known as a context-free
language (a particular kind of formal language).
PARSING
Parsing is essentially the task of determining for a given string of words what
the valid parse trees are with that string as yield. Obviously, only strings in the language will have parse trees,
and thus parsers can be used to determine whether a string is in the language
of a grammar.
Top-down search-based parsing (also known as
recursive descent parsing) is a widely used method for parsing both
computer languages [3] and natural languages [4]. The primary difference between computer languages and natural
languages is that natural language grammars typically admit ambiguity. A typical kind of ambiguity involves
attachment of modifiers, as in the contrast between the attachment of the
prepositional phrases in the following pair of trees that yields the string she
saw the boy with the telescope: [S
[NP she] [VP saw [NP the [N [N boy] [PP with the
telescope]]]]]] versus [S [NP she] [VP [VP saw [NP the [N
boy]]] [PP with the telescope]]] (meaning in the first case that
the boy had the telescope and in the second case, that she did).
The simplest way to define
any search-based algorithm is to provide the search space (see [4], for example). A search space is characterized by a
mapping from an input to a start state, a collection of final states,
and a transition function that takes you from one state to another. For top-down search-based parsing, the
states represent how much of the input string is left and which non-terminals
need to be found. Suppose we have an input
string Ws that we are trying to parse into a tree rooted at non-terminal
S (the start symbol) with respect to a given grammar. Each state in the search space will be of the form Ws / Cs where
Ws is a sequence of words and Cs is a sequence of non-terminals.[2] The search space is:[3]
Start State: Ws / [S]
Final State: [ ] / [ ]
Expand:
Ws / [C0 | Cs] => Ws /
[C1,…,Cn|Cs]
[if C0 => C1,…,Cn
a rule of the grammar]
Match: [W | Ws] / [W | Cs] => Ws / Cs
The list of categories represents things we still need to find, whereas
the list of words represents the words remaining to consume. Thus we start in the state Ws / [S] with all
of the input words remaining and the start-state as the only non-terminal being
sought. The final state represents the
situation in which we have found all of the categories we were looking for and
have consumed all of the input in so doing.
The two transitions in this space correspond to the top-down expansion
of a grammar rule and the matching of input to the grammar. We can expand a category that we are looking
for by replacing it with its daughters in a rule. Similarly, if we are looking for a word and we have that word at
the beginning of the remaining words, we can consume it.
Example:
Suppose we have a very simple grammar for English sentences containing
rules S => NP VP; NP => Det N;
Det => the; N => kid; VP => V; V => ran. Then if we are parsing the string the kid
ran, we have the following sequence of states:
[the, kid, ran] /
[S] start
state
[the, kid, ran] / [NP,
VP] expand S => NP VP
[the, kid, ran] / [Det,
N, VP] expand NP => Det N
[the, kid, ran] / [the,
N, VP] expand Det => the
[kid, ran] / [N,
VP] match the
[kid, ran] / [kid,
VP] expand N => kid
[ran] / [VP] match kid
[ran] / [V] expand
VP => V
[ran] / [ran] expand V => ran
[ ] / [ ]
match ran
As in speech recognition, we are typically interested in all the possible
parses for a given input string.[4] As such, we will need to do an exhaustive
search of the search space (usually known as all-paths parsing). Note that a path through this search space
uniquely determines a parse tree. This
tree can either be constructed from the steps taken during search, or it can be
built online each time a rule is expanded.
Either way, it is the final parse tree from which the semantics will be
computed. Typically, some degree of
lexical lookahead is allowed rather than just blindly expanding rules top-down
hoping to hit upon the right lexical item; this is achieved by only expanding
rules whose right-hand sides begin with words if the appropriate word is there
in the input.
Typically, top-down
search-based parses exclude certain forms of problematic grammars from
consideration. The primary candidates
for exclusion are the left-recursive grammars, because they introduce infinite
loops into the search space.[5] For instance, the left-recursive rule N
=> N PP allows a noun to be followed by a prepositional phrase; this means
that state Ws / [N | Cs] expands to Ws / [N, PP | Cs], which in turn produces
Ws / [N, PP, PP | Cs] and so on ad infinitum. A grammar is said to be left
recursive if there is a sequence of rules[6]
A0 => A1 …; A1 => A2 …; … ; An-1 => An …. Such that
A0=An. So N => N PP is left
recursive with n=1, and the pair A => B C, B => A D is left recursive
with n=2. Left recursive
grammars form the limit case of top-down non-determinism, allowing an infinite
number of states to be reachable from another state without consuming any
input. In general, we define the degree
of ambiguity for a given state to be the number of states that are
reachable from it without consuming any input.
Left recursive grammars have an infinite degree of ambiguity. If a grammar is not left recursive, every
state has a finitely bounded degree of ambiguity. The complexity of search-based parsing is directly proportional
to the number of states that are reachable from the initial state. If every state has a finite degree of
ambiguity, at least that number will be finite. Our goal is to reduce the number of states as much as possible
without damaging the parse tree topology beyond our ability to reconstruct the
semantics from it.
A SIMPLE CASE
Using the parser from SpeechWorks 6.5, we tested the efficiency of three
forms of representing the same grammar.
For the sake of simplicity, we focused on a very common and easily
understood grammar – that for allowing a sequence of between 1 and N instances
of a given non-terminal A. We
considered three ways such a grammar might be written.[7]
Disjunctive Form
S => A; S => A A; S => A A A; S => A
A A A; …
Left “Recursive” Form
S => An; An
=> A; An => An-1
A; An-1 => A; An-1
=> An-2 A; … ; A1 => A
Right “Recursive” Form
S => An; An
=> A; An => A An-1; An-1 => A; An-1 => A An-2; …; A1 => A
Theoretical analysis of the degree of ambiguity of these grammars is
reflected in their empirical run times.
For both the disjunctive and the left “recursive” grammar (it’s not
truly recursive – just a finite approximation of a recursive grammar), parsing
a string of As of length m against a grammar that accepts from 1 to n
instances of non-terminal A results in a number of states on the order of O(n m) to
be explored (see [2] or [5] for a definition of the O notation). For
instance, in the disjunctive case, there are n states expanded before
the first input is consumed, n-1 states expanded at step 2, n-2
states expanded at step 3, and so on up to n-m states expanded after consuming
m inputs, and (n + (n-1) + … + (n-m)) is O(n m). The left “recursive” case is slightly worse.
On the other hand, the number of states explored in the right “recursive”
grammar is linear in the input, or O(m). This is because there are at most two states
explored per input token in the right “recursive” grammar, for a total of 2 + 2
+ … + 2 (m times), which is clearly O(m).[8] We do not consider the doubly recursive
grammar of the form A => A A, which allows any parse tree to be generated;
its complexity is exponential (its given by the Catalan numbers [5]). This case
does arise in natural language through noun compounding, where N => N N, as
in [N [N [N [N towel] [N rack]] [N designer]] [N [N training]
[N courses]]].
Our empirical results support
the theoretical analysis. Using the
SpeechWorks 6.5 parser, we explored grammars accepting between 1 and n words
from a given non-terminal category A.
In Figure 1, we show the results for the three grammars above.[9] We consider the case where the non-terminal
A expands to a set of 256 words, testing against 5000 randomly generated test
with uniformly distributed lengths. Note that the quadratic codings take
roughly 50 times as long to process in longer cases.
A REALISTIC CASE: COUNTING
Although the above case was designed for illustrative simplicity, we have
encountered similar cases in real applications. One example from a real grammar involves agreement between a
keyword and the number of instances. A
precise grammar for this case is: S => A one; S => A A two;
S => A A A three; …. The actual example involved a non-trivial
expansion of the non-terminal A, and a number of subcases, but the above
grammar illustrates the point. As we
saw in Figure 1, simply using the grammar as given above is not particularly
efficient. The obstacle in the way of
directly implementing the right recursive approach above is that we need to
count the number of occurrences and pick up an agreeing word at the end. In order to do this, we can use a grammar of
the following form, in which we represent the count as we proceed down the tree
and make sure we pick up an agreeing element later on. This is achieved with the grammar: S => A S1; S1 => one; S1
=> A S2; S2 => two; S2
=> A S3; … The trick is to simply
use the non-terminals as counters. One
problem is that the resulting tree structure is not what one might expect, but
rather looks like [S [A …] [S1 [A …] [S2 two]]]. In particular, this can cause problems for
the propagation of semantics.
Fortunately, this problem is easily solved if the grammar formalism allows
semantic rules to be attached to the grammar rules, as in standard compilers
(see [3]). For instance, if the word
“two” has some distinguished semantic value, this can simply be propagated by
the rules for S, S1, and S2. In
general, this problem can be handled by a technique known in the programming
literature as continuation passing (see, for example, [6] or [7]).
THE GENERAL CASE
In general, our goal can be seen as simply reducing non-determinism. We can apply two kinds of transforms to our
grammars to convert them to equivalent forms: folding and unfolding,
techniques that are widely employed in optimizing compilers (see [3]). An unfolding is a particular case of a
general technique known as partial evaluation in which one rule is
expanded inside of another. For
instance, it would take A => B C D and C => F that E and produce A
=> B F that E D. A frequent
general case of folding is applied when there are multiple rules that share the
same prefix. In particular, we look for
rules with common prefixes and collapse them. For instance, if we have two
rules A => B C D and A => B C E, then every time we are looking for an A
we expand both rules. We can fold the
repeated sequence B C together with a rule B_C => B C and replace the two
rules above with A => B_C D and A => B_C E. Now only one rule is expanded.
If there is a lot of this kind of duplication, as in our disjunctive
grammar above, the savings can be significant.
Folding and unfolding can be
used to normalize grammars. For instance,
every grammar can be converted to an equivalent grammar with no left recursion,
the so-called Greibach normal form, in which every rule begins with a
word; that is, is of the form A => b C1 … Cn, for n ³ 0.
Unfortunately, it is impossible to fully
determinize all context-free grammars (see [2]); some are intrinsically
ambiguous. Even the simple problem of
context-free grammar equivalence is undecidable [2]. But we can automatically detect a lot of sharing, and unfold an
arbitrary finite amount of duplication.
SUMMARY
We described top-down search-based parsing, and described the measure of ambiguity that directly measures efficiency. We demonstrated how much more efficient grammars are that reduce non-determinism, and provide a general mechanism for writing such grammars and converting existing grammars into more efficient forms.
REFERENCES
[1] SpeechWorks 6.5 Service Creation Guide. 2000. SpeechWorks International, Inc.
[2] J. E. Hopcroft, J. D. Ullman. 1979. Introduction to Automata Theory, Languages and Computation. Addison-Wesley.
[3] Aho, A., R. Sethi, and J. D. Ullman. 1988. Compilers: Principles, Techniques, and Tools. Addison-Wesley.
[4] Jurafsky, D. and J. H. Martin. 2000. Speech and Language Processing. Prentice Hall.
[5] Cormen, T. H., C. E. Leiserson, and R. L. Rivest. 1990. Introduction to Algorithms. MIT Press.
[6] Norvig, P. 1992. Paradigms of Artificial Intelligence Programming. Morgan-Kaufmann.
[7] Johnson, M. 1995. Memoization in Top-down Parsing. Computational Linguistics 21:3, 405-418.
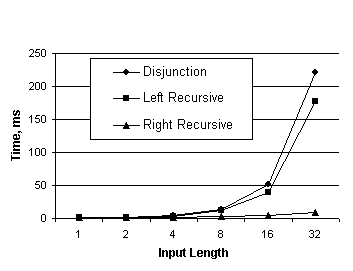 Figure 1. Time vs.
Input Length for different codings.
Figure 1. Time vs.
Input Length for different codings.